MinersAI

Advancements in modern geochemical sampling methods have allowed for highly detailed, large-scale datasets to become a part of the exploration geologist’s toolkit. As these datasets grow larger and more complex, the need has arisen for optimized, accurate, and accessible analytical models to improve the odds of exploration projects. In a recent open-source code release, MinersAI presents a comparative evaluation of three machine-learning based multivariate anomaly detection techniques applied to high-dimensional geochemical data (Howe 2025).

Evaluating Machine Learning Models for Multivariate Anomaly Detection in Mineral Exploration

Building on the work of Antione Caté on multivariate outlier detection (Caté 2025), MinersAI recently conducted a study to explore three machine learning multivariate anomaly detection models, analyzing and comparing both their accuracy and efficiency. Utilizing extensive geochemical datasets from Southeastern Alaska and Southwestern Saudi Arabia, we evaluated the performance of Isolation Forest (IF), Local Outlier Factor (LOF), and Angle-Based Outlier Detection (ABOD), aiming to provide a framework to guide method selection in geoscience and mineral exploration.

Anomaly score map from the Isolation Forest model run on the Alaska dataset. Lower anomaly score values indicate a higher likelihood of being an outlier.

Model Breakdown: Isolation Forest, Local Outlier Factor, and Angle-Based Outlier Detection

Isolation Forest, a model based on binary tree partitioning, quickly and effectively isolates outliers by segmenting data points and tracking features that require the fewest number of splits to isolate (Liu et al. 2008). Local Outlier Factor uses local density metrics, comparing the density of data points in their neighborhoods, with anomalies presenting as isolated or marginalized samples (Breunig et al. 2000). Angle-Based Outlier Detection compares the distribution of angles of distance vectors between a sample point and its neighbors, with smaller angle distributions indicating possible outliers (Kriegel et al. 2008).

Performance Evaluation: Balancing Accuracy and Computational Efficiency

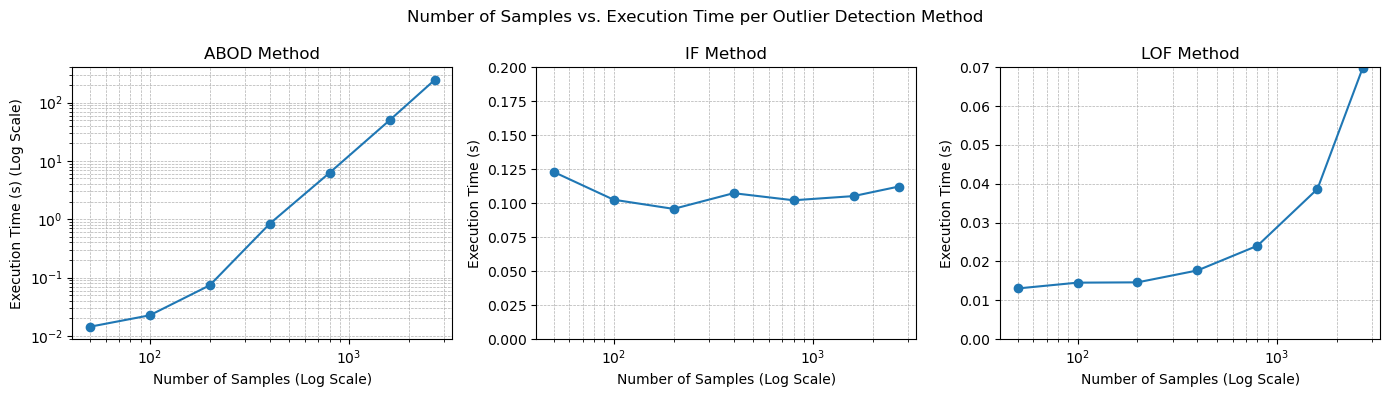
Our two-part analysis investigated both the accuracy and computational efficiency of each of these models, attempting to find an optimal balance between model accuracy and time cost to aid in efficient and effective exploration. Our results demonstrate that ABOD had the highest level of accuracy, most directly aligning predicted anomalies with known regions of mineralization, but also highlighted its significant computational cost, especially in larger datasets. Conversely, IF proved to be a balanced choice for large-scale projects, providing reliable accuracy at greatly reduced processing times. LOF failed to keep up with ABOD and IF in accuracy, and had a slightly higher time cost than IF, and thus was deemed not as applicable to such geochemical applications.

Receiver Operating Characteristic (ROC) curves for each of the models, further illustrating the hierarchy of accuracy between models, with ABOD performing the best, followed by IF then LOF. The more a model is skewed towards the upper left of the graph, the better it balances accurate predictions.

Time complexity plots of each model. IF and LOF execution times are short enough that there is high variability between model runs; regardless, they remain well below 1 second regardless of sample size. ABOD demonstrates a clear O(n2) time complexity at the minute scale over n=1000.

By utilizing these anomaly detection techniques, MinersAI transforms raw geochemical data into actionable insights to guide exploration efforts toward the most promising targets. Combined with our other advanced machine learning analytical tools, our approach to mineral exploration enhances decision-making speed, reduces resource waste, and increases the likelihood of success.

‍

References

Breunig, M.M., Kriegel, H.-P., Ng, R.T., and Sander, J., 2000, LOF: Identifying density-based local outliers: ACM SIGMOD Record, v. 29, no. 2, p. 93–104. https://doi.org/10.1145/335191.335388

Caté, A., 2025, 6: Multivariate outlier detection for mineral exploration: LinkedIn Pulse, accessed February, 2025, at https://www.linkedin.com/pulse/6-multivariate-outlier-detection-mineral-exploration-antoine-caté-vd4kc/.

Howe, Tyler and MinersAI, 2025. Multivariate Outlier Detection in Geochemical Datasets. GitHub repository. Available at: https://github.com/MinersAI/geochemical_anomaly_detection

Kriegel, H.-P., Schubert, M., and Zimek, A., 2008, Angle-based outlier detection in high-dimensional data: Proceedings of the 14th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, Las Vegas, Nevada, USA, Association for Computing Machinery, p. 444–452. https://doi.org/10.1145/1401890.1401946.

Liu, F.T., Ting, K.M., and Zhou, Z.-H., 2008, Isolation Forest: Eighth IEEE International Conference on Data Mining, p. 413–422. https://doi.org/10.1109/ICDM.2008.17.

‍

ML Anomaly Detection for Smarter Mineral Exploration